Числа

Числа в математике

Изначально компьютеры создавались как машины, выполняющие вычисления. Само слово "компьютер" означает "вычислитель". Ранее у нас в стране для обозначения компьютеров использовалась аббревиатура ЭВМ – Электронная Вычислительная Машина.

Сегодня компьютеры – это машины, обрабатывающие информацию. Эта информация может быть представлена данными самого разного вида – текстами, графикой, видео и аудио. Но и сегодня числа являются основным видом данных, с которыми работает компьютер. Так или иначе все виды данных отображаются в числа. Справедливо полагать, что компьютер может оперировать только с нулями и единицами. Вся информация, обрабатываемая компьютером, представляет последовательности символов, представляющие две цифры – ноль и единицу.

Математика с давних пор изучает числа. Самый простой и естественный вид чисел – это целые положительные числа, которые издавна использовались для обозначения количества предметов (один, два и так далее) и порядка следования предметов (первый, второй и так далее). Такие числа в математике называются натуральными. В математике есть некоторый спор, является ли число "ноль" натуральным? Мы будем относить 0 к натуральным числам. Натуральных чисел бесконечно много. За каждым натуральным числом следует число, на единицу больше предыдущего. Для обозначения бесконечности ряда натуральных чисел в математике придуман специальный символ бесконечности - .

Натуральные числа: 0, 1, 2, …, 10, 11, 12, ..., 1000, 1001, 1002, ....

Следующий вид чисел – это целые числа, которые могут быть как положительными, так и отрицательными.

Целые числа: ... -2, -1, 0, 1, 2, ....

Следующий вид чисел – это дробные числа. Рациональные числа – это дроби вида m/n, где m и n – это целые числа. Одно и тоже рациональное число может быть представлено бесконечным числом дробей, например, 1/2 = 2/4 = -2/-4 = 3/6 = ... = 100/200 = ... = 2000/4000 = ....

Единственным представителем множества равных рациональных чисел является число, представленное дробью - m/n, где m и n взаимно несократимы. Для приведенного выше ряда таким представителем является дробь 1/2 ..

Рациональные числа чаще всего записывают в виде десятичного числа с целой и дробной частью. Например, рациональное число 1/2 представимо числом 0,5, а рациональное число 12/5 представимо числом 2,4. Для некоторых рациональных чисел дробная часть десятичного числа может быть представлена бесконечной периодической дробью. Например, рациональное число 1/3 представимо десятичным числом 0,6666666..., что записывают в виде 0,(6).

В результате выполнения некоторых операций над числами могут появляться новые виды чисел, не являющиеся ни целыми, ни рациональными. Иррациональные числа – это числа, представленные десятичным числом, дробная часть которых является бесконечной непериодической дробью. Такие числа существуют. Наиболее известным примером иррационального числа является число, имеющее собственное имя, – число 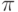, задающее отношение длины окружности к ее диаметру. Это отношение не может быть выражено никаким рациональным, тем более целым числом. Другим классическим примером иррациональных чисел являются числа вида 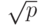, где p – простое число.

Натуральные, целые, рациональные и иррациональные числа называют вещественными числами. Но некоторые операции над вещественными числами приводят к числам, не являющихся вещественными. Извлечение корня квадратного корня из отрицательных чисел приводит к числам, называемых 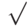мнимыми. Число 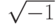называется мнимой единицей и обозначается латинской буквой i. Числа вида a+b*i называются комплексными, где a и b – это вещественные числа, i – мнимая единица.

Давайте докажем, что 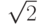– число иррациональное. Для доказательства истинности этого утверждения будем использовать метод доказательства, называемый методом доказательства "от противного".

Теорема (о существовании иррациональных чисел)

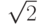– число иррациональное.

Доказательство (от противного).

Предположим, что 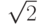- число рациональное, то есть 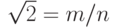(m, n целые, взаимно несократимые числа), следовательно 2 = m²/n², и n²= m²/2, значит m² делится нацело на 2 и m² – число четное и m – число четное (квадрат нечетного числа является нечетным числом), следовательно m = 2*k и m² = 4*k², а значит и k²= n²/2, то есть n делится нацело на 2 и m и n взаимно сократимы.

Пришли к противоречию. Утверждение "m и n взаимно сократимы" ложно. Отсюда следует, что и исходная посылка вывода "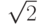 - число рациональное" является ложным утверждением. Следовательно, √2 не является рациональным числом. Число 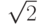- вещественное иррациональное число. Оно представимо бесконечной непериодической дробью.

Доказательство от противного основано на законах логики. Пусть Q утверждение некоторой теоремы. Доказательство истинности утверждения Q строится следующим образом. Предположим противное, полагая, что утверждение теоремы Q ложно, а истинным является отрицание Q. Если из отрицания Q в результате правильно построенных выводов приходим к заключению, которое является ложным, то по законам логики отрицание Q является ложным, а, следовательно, утверждение теоремы Q является истинным.

Доказательство основано на свойстве логической операции, называемой импликацией или операции следования Q → R (посылка Q влечет заключение R). Когда импликация истинна (вывод построен корректно), а заключение ложно, то это может быть только в том случае, если посылка Q ложна. Подробнее об импликации и законах логики можно прочесть в моем курсе для школьников "Введение в логику", опубликованном на сайте Интернет университета ИТ (intuit.ru).

Числа в программировании

В программировании числа устроены проще чем в математике. Конечно, есть целые числа и компьютеры могут выполнять различные операции над целыми числами. Но множество целых чисел является конечным множеством – это числа из некоторого конечного интервала. Обычно в программировании целые числа делятся на подтипы. Каждый подтип характеризуется своим интервалом, содержащим целые числа. Мы с вами будем писать программы на языке C#, в котором довольно много различных подтипов целых чисел. Но на первом этапе нам достаточно использовать один подтип целых чисел, называемый типом int (от слова integer – целое). Типу int принадлежат целые числа из интервала –[- 2³¹ - +2³¹ – 1]. В этот интервал попадают все целые положительные и отрицательные числа от 0 до двух миллиардов. Для большинства задач чисел из этого диапазона вполне достаточно.

Конечно же, в программировании можно работать и с десятичными числами, имеющими целую и дробную часть. Но и здесь рассматривается конечное множество чисел, каждое из которых имеет конечное число цифр. Никаких бесконечных непериодических и периодических дробей в программировании нет. Десятичные числа в программировании называются вещественными и также разделяются на подтипы. Опять-таки, на первых порах мы будем использовать один подтип, называемый в языке C# типом double. Числа этого типа можно представить в виде 0,q*10^p. Здесь q называется мантиссой числа, а p – десятичным порядком. Числа этого типа находятся в интервале [- 1,79769313486232*10³⁰⁸ - +1,79769313486232*10³⁰⁸].

Мантисса таких чисел содержит 16-17 значащих цифр, а порядок находится в пределах далеко выходящих за порядок чисел, используемых в обычных задачах. Заметим, что порядок может быть также отрицательным числом.

В мире чисел, рассматриваемых в программировании, нет бесконечности и нет иррациональности. С чем связано это ограничение? Дело в том, что числа хранятся в памяти компьютера. Память имеет ограниченные размеры, в ней нужно хранить большое число различных данных. Поэтому для чисел отводится память конечного размера. Размер отводимой памяти для хранения чисел того или иного типа (подтипа), определяет интервал чисел этого типа.