Анализ игр
11.2. Цена игры
Анализируя игры в предыдущем разделе, мы использовали следующие (очевидные) правила:
- Если из некоторой позиции
 можно пойти (по стрелкам)
в некоторую проигрышную (для попавшего в нее игрока)
позицию, то позиция
можно пойти (по стрелкам)
в некоторую проигрышную (для попавшего в нее игрока)
позицию, то позиция  является выигрышной (для попавшего
в нее).
является выигрышной (для попавшего
в нее). - Если из некоторой позиции
 можно пойти только
в выигрышные позиции, то позиция
можно пойти только
в выигрышные позиции, то позиция  является проигрышной.
является проигрышной.
11.2.1. Доказать, что если число позиций в игре конечно, нет циклов (нельзя вернуться в однажды пройденную позицию) и про все заключительные позиции (где нельзя сделать хода) известно, кто выигрывает, то правила 1 и 2 однозначно разбивают все позиции на выигрышные и проигрышные.
Решение. Будем применять эти правила, пока это возможно. Ясно, что никакая позиция не будет объявлена одновременно выигрышной и проигрышной (для попавшего в нее). Надо лишь доказать, что не останется "сомнительных" позиций (не отнесенных ни к выигрышным, ни к проигрышным). Заметим, что из каждой сомнительной позиции ведет стрелка хотя бы в одну сомнительную позицию. (В самом деле, если все стрелки ведут в несомненные позиции, то либо все они выигрышные, либо есть хоть одна проигрышная, и можно было бы воспользоваться одним из двух правил.) Значит, идя по стрелкам в сомнительные позиции, мы рано или поздно получим цикл, что противоречит предположению.
11.2.2. Сформулировать и доказать аналогичное утверждение для игр, допускающих ничьи.
Игры с ничейным исходом являются частными случаями конечных игр с полной информацией и нулевой суммой, рассматриваемых в теории игр. Чтобы задать такую игру, необходимо:
- указать конечное множество, элементы которого называются позициями;
- для каждой позиции указать, является ли она заключительной (игра закончена) или нет;
- для каждой заключительной позиции указать результат игры (число); это число понимается как сумма денег, которую один игрок платит другому;
- для каждой незаключительной позиции указать, кто из игроков должен делать ход в этой позиции и какие разрешены ходы (в какие позиции этот игрок может перейти);
- указать начальную позицию игры.
При этом требуется, чтобы не было циклов (нельзя было вернуться в уже пройденную позицию после нескольких ходов).
Позиции игры удобно рассматривать как вершины графа и изображать точками; возможные ходы при этом становятся ребрами графа и изображаются стрелками. Игру можно рассматривать как передвижение фишки, обозначающей текущую позицию игры, по этому графу. В каждой вершине написано, кто должен делать ход (если игра не кончилась) или кто и сколько выиграл (если игра кончилась). Одна из вершин указана как начальная позиция.
Будем называть игроков Макс и Мин и считать, что результат игры определяет, сколько Мин платит Максу. (Мотивировка: Макс хочет, чтобы это число было максимальным, а Мин - минимальным - а лучше всего отрицательным, поскольку тогда он получает деньги!) Кто из игроков делает первый ход, определяется начальной позицией. Заметим, что мы теперь не предполагаем, что игроки ходят по очереди: один и тот же игрок может делать несколько ходов подряд.
(Тем самым, например, в игре со спичками каждый кружок на рисунке 11.1 теперь превращается в две позиции: с ходом Макса и с ходом Мина.)
Игра, в которой один из игроков выигрывает, а другой
проигрывает, соответствует значениям  в заключительных вершинах (
в заключительных вершинах ( 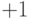 означает выигрыш Макса,
означает выигрыш Макса, 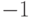 означает выигрыш Мина). Игры с ничейными исходами
получатся, если приписать число
означает выигрыш Мина). Игры с ничейными исходами
получатся, если приписать число  ничейным позициям.
ничейным позициям.
Определим теперь понятие стратегии. Стратегия
для Макса (или Мина) определяет, как он должен
ходить в каждой из позиций (где ход за ним); формально это
функция  , определенная на множестве позиций, где ход за
ним. Значениями этой функции являются позиции, при этом
ходы должны быть допустимыми, то есть из
, определенная на множестве позиций, где ход за
ним. Значениями этой функции являются позиции, при этом
ходы должны быть допустимыми, то есть из  в
в 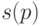 должна вести стрелка.
должна вести стрелка.
Стратегии такого типа называют в теории игр позиционными, подчеркивая, что выбор хода зависит лишь от текущей позиции, но не от истории игры (как мы в эту позицию попали). (Другие стратегии нам не понадобятся, так что слово "позиционная" мы будем опускать.)
Если фиксировать стратегии для Макса и Мина, то исход игры предопределен: эти стратегии однозначно определяют последовательность позиций ("партию") и результат игры.
11.2.3.
Доказать, что для любой игры 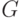 можно найти число
можно найти число  и стратегии
и стратегии  и
и  для Макса и Мина, при которых:
для Макса и Мина, при которых:
(1) Макс, пользуясь стратегией  , гарантирует себе
выигрыш не менее
, гарантирует себе
выигрыш не менее  , как бы ни играл Мин;
, как бы ни играл Мин;
(2) Мин, пользуясь стратегией  , гарантирует себе
проигрыш не более
, гарантирует себе
проигрыш не более  , как бы ни играл Макс.
, как бы ни играл Макс.
Число  называют ценой игры
называют ценой игры 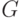 .
Заметим, что цена игры
определяется однозначно: из условий
(1) и (2) следует, что у Макса нет стратегии, гарантирующей
ему выигрыш больше
.
Заметим, что цена игры
определяется однозначно: из условий
(1) и (2) следует, что у Макса нет стратегии, гарантирующей
ему выигрыш больше  (поскольку она не может это сделать
против стратегии
(поскольку она не может это сделать
против стратегии  ), а у Мина нет стратегии,
гарантирующей ему проигрыш меньше
), а у Мина нет стратегии,
гарантирующей ему проигрыш меньше  .
.
Для игр с двумя исходами утверждение задачи (называемое теоремой Цермело означает, что ровно у одного из игроков имеется выигрышная стратегия. Если разрешить и ничьи, то либо у одного из игроков есть выигрышная стратегия, либо у обоих есть стратегия, гарантирующая ничью.
Решение. Пусть  - произвольная позиция
игры
- произвольная позиция
игры 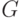 .
Рассмотрим игру
.
Рассмотрим игру 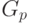 , которая отличается от
, которая отличается от 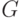 лишь
начальной позицией, и эта начальная позиция есть
лишь
начальной позицией, и эта начальная позиция есть  . (Если
. (Если  - заключительная вершина, то игра
- заключительная вершина, то игра 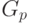 тривиальна:
игра кончается, не начавшись, и игрокам сообщается
результат игры.) Как мы сейчас увидим, цену игры
тривиальна:
игра кончается, не начавшись, и игрокам сообщается
результат игры.) Как мы сейчас увидим, цену игры 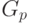 (как
функцию от
(как
функцию от  ) можно определить рекурсивно, начиная
с заключительных позиций.
) можно определить рекурсивно, начиная
с заключительных позиций.
Более точно, рассмотрим следующее рекурсивное определение
некоторой функции  , определенной на вершинах графа:
, определенной на вершинах графа:
-
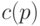 равно выигрышу Макса (=проигрышу Мина)
в позиции
равно выигрышу Макса (=проигрышу Мина)
в позиции  ,
если позиция
,
если позиция  является заключительной;
является заключительной; -
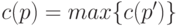 , если в вершине
, если в вершине  ходит Макс;
максимум
берется по всем вершинам
ходит Макс;
максимум
берется по всем вершинам 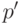 , в которые Макс может пойти
из
, в которые Макс может пойти
из  по правилам игры;
по правилам игры; -
 , если в вершине
, если в вершине  ходит Мин;
минимум
берется по всем вершинам
ходит Мин;
минимум
берется по всем вершинам 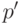 , в которые Мин может пойти
из
, в которые Мин может пойти
из  по правилам игры.
по правилам игры.
Лемма. Это определение корректно: существует
и единственна функция  (аргументы - вершины графа,
значения - числа), удовлетворяющая указанным требованиям.
(аргументы - вершины графа,
значения - числа), удовлетворяющая указанным требованиям.
Доказательство леммы. Назовем рангом вершины
максимальное число ходов, которое можно сделать из этой
вершины. Поскольку по предположению в игре нет циклов, то ранг любой вершины не больше числа вершин. Докажем
индукцией по  , что существует и единственна
функция
, что существует и единственна
функция  ,
определенная на вершинах ранга не больше
,
определенная на вершинах ранга не больше  и удовлетворяющая рекурсивному определению. Для
и удовлетворяющая рекурсивному определению. Для 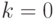 это
очевидно. Шаг индукции использует такое (очевидное)
замечание: если из вершины
это
очевидно. Шаг индукции использует такое (очевидное)
замечание: если из вершины  можно сделать ход
в вершину
можно сделать ход
в вершину 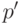 , то ранг вершины
, то ранг вершины 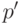 меньше ранга
вершины
меньше ранга
вершины  . Поэтому рекурсивное определение однозначно
задает значения на вершинах ранга
. Поэтому рекурсивное определение однозначно
задает значения на вершинах ранга  , если известны значения на вершинах меньших рангов. Лемма доказана.
, если известны значения на вершинах меньших рангов. Лемма доказана.
Осталось доказать, что значение 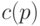 является ценой
игры
является ценой
игры 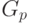 . Рассмотрим следующую (позиционную) стратегию
для Макса: из вершины
. Рассмотрим следующую (позиционную) стратегию
для Макса: из вершины  ходить в ту вершину
ходить в ту вершину 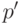 , для
которой значение
, для
которой значение 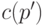 максимально (и равно
максимально (и равно 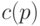 ).
Если
Макс следует этой стратегии, то независимо от ходов Мина
значение
).
Если
Макс следует этой стратегии, то независимо от ходов Мина
значение 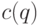 для текущей вершины
для текущей вершины  не убывает в ходе
игры (при ходах Мина оно убывать вообще не может, при ходах
Макса оно не убывает по построению стратегии). Тем самым
в вершине
не убывает в ходе
игры (при ходах Мина оно убывать вообще не может, при ходах
Макса оно не убывает по построению стратегии). Тем самым
в вершине  Максу гарантирован выигрыш не
меньше
Максу гарантирован выигрыш не
меньше 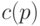 .
Аналогичным образом, если Мин ходит в ту вершину
.
Аналогичным образом, если Мин ходит в ту вершину 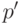 , где
достигается минимум
, где
достигается минимум 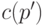 (равный
(равный 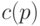 ), то значение
), то значение 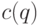 не возрастает в ходе игры и потому Мин проигрывает
не более
не возрастает в ходе игры и потому Мин проигрывает
не более 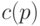 .
.
Теорема Цермело доказана.
