Сопоставление с образцом
Подведем итоги. Рассмотренный способ хранения деревьев
позволяет (для фиксированного слова  )
)
- создать дерево из одного корня [
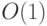 ];
]; - найти отца любой вершины (кроме корня) [
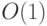 ];
]; - узнать пометку любой вершины (кроме корня), то есть
пометку ведущего к ней ребра [
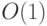 ];
]; - пройти из любой позиции
 вдоль любого слова
вдоль любого слова  ,
если заранее известно, что мы не выйдем из дерева; результатом является позиция
,
если заранее известно, что мы не выйдем из дерева; результатом является позиция  в дереве, для которой
в дереве, для которой 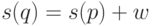 [ O (число ребер на пути)];
[ O (число ребер на пути)]; - добавить слово
 , начав с позиции
, начав с позиции  ; если при
этом слово
; если при
этом слово  является подсловом
является подсловом  , а в дереве нет позиции
, а в дереве нет позиции  , для которой
, для которой 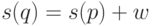 , то дерево
меняется и такая позиция
, то дерево
меняется и такая позиция  создается (она будет
листом) [ O (число букв в w, не вошедших
в l(q) ];
создается (она будет
листом) [ O (число букв в w, не вошедших
в l(q) ]; - наконец, для любого слова
 можно выяснить, найдется ли
в дереве позиция
можно выяснить, найдется ли
в дереве позиция  , для которой
, для которой 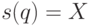 [
[ 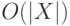 ].
].
В квадратных скобках указано число действий при выполнении соответствующих операций.
Еще мы будем хранить в вершинах дерева " суффиксные ссылки " (в каждой вершине будет не более одной ссылки на другую вершину), но сначала надо объяснить, что это такое.
Начнем с полного (не сжатого) суффиксного дерева для
слова  . Каждой его вершине (кроме корня) отвечает
некоторое непустое подслово слова
. Каждой его вершине (кроме корня) отвечает
некоторое непустое подслово слова  . Если мы отрежем
у этого подслова последнюю букву, то в дереве спустимся на
один шаг к корню. Но что будет, если мы отрежем первую
букву? Снова получится подслово, но оно уже будет совсем
в другом месте дерева.
. Если мы отрежем
у этого подслова последнюю букву, то в дереве спустимся на
один шаг к корню. Но что будет, если мы отрежем первую
букву? Снова получится подслово, но оно уже будет совсем
в другом месте дерева.
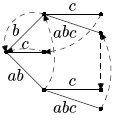
Вот как выглядят эти переходы в нашем примере (отрезание первой буквы соответствует пунктирной стрелке):
Эти стрелки мы будем называть суффиксными ссылками, поскольку они соответствуют переходу от слова к его суффиксу на единицу меньшей длины. Они определены для всех вершин, кроме корня.
Формально можно сказать так. Пусть 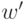 означает
слово
означает
слово  без первой буквы (
без первой буквы ( 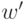 определено для любого непустого
слова
определено для любого непустого
слова  ). Тогда суффиксная ссылка ведет из вершины
). Тогда суффиксная ссылка ведет из вершины  в вершину
в вершину  , если
, если  (напомним, что
(напомним, что 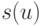 - слово, соответствующее вершине
- слово, соответствующее вершине  ).
).
10.8.5. Как связаны суффиксные ссылки двух соседних вершин (отца и сына)?
Ответ. Они указывают на соседние вершины, и буква на соединяющем их ребре та же самая.
10.8.6. Доказать, что при переходе к сжатому суффиксному дереву ссылки по-прежнему идут из вершины в вершину (а не внутрь ребер).
Решение. В самом деле, по нашему предположению последняя
буква слова больше в нем не встречается, поэтому из листа
ссылка ведет в лист. А если вершина (отличная от корня)
является точкой ветвления, то соответствующее ей слово  встречается с различными буквами после него. Другими
словами, для некоторых букв
встречается с различными буквами после него. Другими
словами, для некоторых букв  и
и  слова
слова 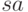 и
и 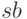 являются подсловами слова
являются подсловами слова  . Отрезав от них первую букву,
получим слова
. Отрезав от них первую букву,
получим слова 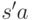 и
и 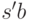 , которые также являются
подсловами слова
, которые также являются
подсловами слова  , поэтому и
, поэтому и 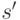 является точкой
ветвления.
является точкой
ветвления.
Вот что получится для нашего примера:
Теперь мы уже готовы к изложению алгоритма МакКрейта. Сжатое суффиксное дерево строим постепенно, добавляя к нему
суффиксы по мере уменьшения их длины. Обозначим через 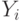 суффикс, начинающийся с
суффикс, начинающийся с  -ой буквы слова
-ой буквы слова  . (Таким
образом,
. (Таким
образом,  , а
, а 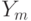 состоит из одной буквы.) После
состоит из одной буквы.) После  шагов построения наше дерево будет хранить
шагов построения наше дерево будет хранить 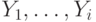 .
.
10.8.7.
Показать, что суффиксные ссылки в таком дереве определены
корректно (ведут в другую вершину того же дерева) для всех
вершин, кроме, возможно, последнего добавленного листа
(соответствующего слову 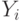 ) и его отца.
) и его отца.
Решение.
В самом деле, суффиксная ссылка из листа 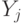 ведет
в лист
ведет
в лист 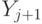 , и потому ей есть куда вести. Рассмотрим
теперь внутреннюю вершину
, и потому ей есть куда вести. Рассмотрим
теперь внутреннюю вершину 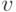 , не являющуюся отцом
последнего листа. Пусть в ней разветвляются два пути
в листья
, не являющуюся отцом
последнего листа. Пусть в ней разветвляются два пути
в листья 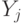 и
и 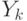 . Без ограничения общности можно
считать, что
. Без ограничения общности можно
считать, что 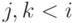 (если один из путей ведет в
(если один из путей ведет в 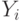 ,
то его можно заменить другим, ведь вершина
,
то его можно заменить другим, ведь вершина 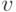 по
предположению не последняя развилка на этом пути). Отрезав
от этих путей первый символ, получим пути
в листья
по
предположению не последняя развилка на этом пути). Отрезав
от этих путей первый символ, получим пути
в листья 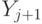 и
и 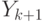 ; эти пути присутствуют
в дереве (поскольку
; эти пути присутствуют
в дереве (поскольку  и
и  не
превосходят
не
превосходят  ),
а точка их развилки будет концом суффиксной ссылки вершины
),
а точка их развилки будет концом суффиксной ссылки вершины 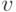 .
.
Суффиксные ссылки для листьев нам не понадобятся,
и вычислять мы их не будем, а для всех остальных вершин
дерева мы их будем вычислять и хранить. Более точно, после  шагов алгоритма
шагов алгоритма


 (и все их начала);
(и все их начала); ;
;