Как обойтись без рекурсии
8.3. Более сложные случаи рекурсии
Пусть функция  с натуральными аргументами и значениями
определена рекурсивно условиями
с натуральными аргументами и значениями
определена рекурсивно условиями
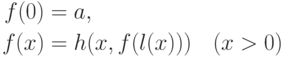
 - некоторое число, а
- некоторое число, а  и
и 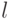 -
известные функции.
Другими словами, значение функции
-
известные функции.
Другими словами, значение функции  в точке
в точке  выражается через значение
выражается через значение  в точке
в точке 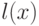 . При этом
предполагается, что для любого
. При этом
предполагается, что для любого  в последовательности
в последовательности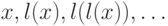
 .
.Если дополнительно известно, что 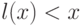 для
всех
для
всех  ,
то вычисление
,
то вычисление  не представляет труда: вычисляем
последовательно
не представляет труда: вычисляем
последовательно 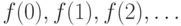
8.3.1.
Написать нерекурсивную программу вычисления  для общего
случая.
для общего
случая.
Решение. Для вычисления  вычисляем
последовательность
вычисляем
последовательность

 в точках этой последовательности, идя справа
налево.
в точках этой последовательности, идя справа
налево.Еще более сложный случай из следующей задачи вряд ли
встретится на практике (а если и встретится, то проще
рекурсию не устранять, а оставить). Но тем не менее: пусть
функция  с натуральными аргументами и значениями
определяется соотношениями
с натуральными аргументами и значениями
определяется соотношениями
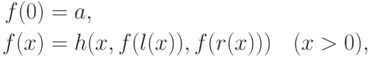
 - некоторое число, а
- некоторое число, а 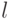 ,
,  и
и  - известные
функции. Предполагается, что если взять произвольное число
и начать применять к нему функции
- известные
функции. Предполагается, что если взять произвольное число
и начать применять к нему функции 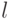 и
и  в произвольном
порядке, то рано или поздно получится
в произвольном
порядке, то рано или поздно получится  .
.8.3.2.
Написать нерекурсивную программу вычисления  .
.
Решение. Можно было бы сначала построить дерево,
у которого в корне находится  , а в сыновьях
вершины
, а в сыновьях
вершины  стоят
стоят 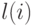 и
и 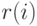 - если только
- если только  не
равно нулю.
Затем вычислять значения функции, идя от листьев к корню.
Однако есть и другой способ.
не
равно нулю.
Затем вычислять значения функции, идя от листьев к корню.
Однако есть и другой способ.
Обратной польской записью (или постфиксной записью ) выражения называют запись, где знак функции стоит после всех ее аргументов, а скобки не используются. Вот несколько примеров:
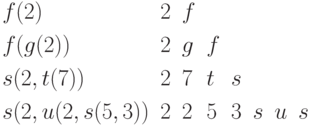
 .
Этот калькулятор имеет стек, который мы будем представлять
себе расположенным горизонтально (числа вынимаются
и кладутся справа), и клавиши - числовые и функциональные.
При нажатии на клавишу с числом это число кладется в стек.
При нажатии на функциональную клавишу соответствующая
функция применяется к нескольким аргументам у вершины
стека. Например, если в стеке были числа
.
Этот калькулятор имеет стек, который мы будем представлять
себе расположенным горизонтально (числа вынимаются
и кладутся справа), и клавиши - числовые и функциональные.
При нажатии на клавишу с числом это число кладется в стек.
При нажатии на функциональную клавишу соответствующая
функция применяется к нескольким аргументам у вершины
стека. Например, если в стеке были числа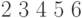
 , соответствующая
функции от двух аргументов, то в стеке окажутся числа
, соответствующая
функции от двух аргументов, то в стеке окажутся числа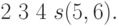
Перейдем теперь к нашей задаче. В процессе вычисления
значения функции  мы будем работать со стеком чисел,
а также с последовательностью чисел и символов f, l, r, h, которую мы будем интерпретировать как
последовательность нажатий клавиш на стековом калькуляторе.
Инвариант такой:
мы будем работать со стеком чисел,
а также с последовательностью чисел и символов f, l, r, h, которую мы будем интерпретировать как
последовательность нажатий клавиш на стековом калькуляторе.
Инвариант такой:

 . Тогда
вначале мы помещаем в стек число
. Тогда
вначале мы помещаем в стек число  , а последовательность
содержит единственный символ f. (При этом инвариант
соблюдается.) Далее с последовательностью и стеком
выполняются такие преобразования:
, а последовательность
содержит единственный символ f. (При этом инвариант
соблюдается.) Далее с последовательностью и стеком
выполняются такие преобразования:![{\hss
\begin{array}{llll}
{старый} & {старая}& {новый} & {новая}
\\[-.5ex]
{стек} & {последовательность}&{стек} &{последовательность}
\\[1ex]
%
X\ & x\ P & X\ x & P\\
X\ x & {l}\ P & X\ l(x) & P\\
X\ x & {r}\ P & X\ r(x) & P \\
X\ x\ y\ z& {h}\ P & X\ h(x,y,z) & P \\
X\ 0 & {f}\ P & X\ a & P \\
X\ x & {f}\ P & X & x\ x\ {l}\ {f}\ x\ {r}\ {f}\
{h}\ P
\end{array}\hss}](/sites/default/files/tex_cache/8b78a14a434ae2d0a458130958a60735.png)
 ,
,  ,
,  - числа,
- числа,  -
последовательность
чисел,
-
последовательность
чисел, 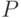 - последовательность чисел и символов f, l, r, h. В последней строке предполагается, что
- последовательность чисел и символов f, l, r, h. В последней строке предполагается, что 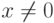 . Эта строка соответствует равенству
. Эта строка соответствует равенству
Замечание. Последовательность по существу представляет собой стек отложенных заданий (вершина которого находится слева).
