НОУ ИНТУИТ | Основы программирования на С# 3.0: ядро языка. Лекция 5: Процедуры и функции

Тверской государственный университет

Опубликован: 02.12.2009 | Доступ: свободный | Студентов: 3459 / 692 | Оценка: 4.41 / 4.23 | Длительность: 09:18:00

ISBN: 978-5-9963-0259-8

Тема: Программирование

Специальности: Программист, Архитектор программного обеспечения

Вам нравится? Нравится 36 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Задачи и алгоритмы

Слово, число, рисунок, нота- величайшие изобретения человечества. Для программистов это информационные объекты, с которыми нужно уметь оперировать.

Числа

Алгоритмы и задачи, рассматриваемые в этой главе, можно использовать на начальном этапе обучения программированию при изучении простейшего вида модульности - процедур и функций.

Многие задачи этой главы являются хорошими примерами при изучении темы классов. У класса двойственная природа - с одной стороны, это модуль, с другой - тип данных. Рациональные числа, комплексные числа, простые числа являются естественными примерами классов, поскольку интуитивно понятно, какой тип данных они задают.

Цифры. Системы счисления

Для записи чисел привычным способом, знакомым еще с первых классов школы, является их запись в позиционной системе счисления. Напомним некоторые факты. В позиционной системе счисления всегда есть цифра 1. Считается, что единицу создал бог, а остальные цифры придуманы человеком. Если так, то наиболее замечательной из человеческих придумок в этой области является введение цифры 0. Цифры позиционной системы упорядочены, и каждая получатся из предыдущей прибавлением единицы. Число различных цифр в позиционной системе счисления задает основание системы счисления - . В привычной для нас десятичной системе счисления p = 10 и цифрами являются знакомые всем символы: 0, 1, 2, … 9. В двоичной системе счисления цифр всего две - 0 и 1 и p = 2. В шестнадцатеричной системе счисления p =16, и привычных символов для обозначения цифр не хватает, так что дополнительно используются большие буквы латинского алфавита: 0, 1, 2, … 9, A, B, C, D, E, F, где A задает 10, а F - цифру 15. Поскольку в любой позиционной системе счисления цифры задают числа от 0 до p-1, для числа p уже нет специального символа. Как следствие, в любой позиционной системе счисления основание системы счисления представляется числом 10, так что справедливы следующие соотношения: $2_{(10)} = 10_{(2)}; 16_{(10)} = 10_{(16)}; p_{(10)} = 10_{(p)}$ . Здесь и в дальнейшем при записи числа при необходимости будем указывать в круглых скобках и систему счисления. В обыденной жизни непреложным фактом является утверждение "2*2=4". Мы понимаем, что столь же верным является утверждение "2*2 = 11" (в троичной системе счисления), или, если хотите, "2*2 = 10", - все зависит от системы счисления, в которой ведутся вычисления.

Еще Эйлер занимался записью чисел в различных системах счисления. В его записных книжках можно найти запись числа 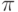$\pi$ в двоичной системе счисления и запись чисел в системе с основанием 24, цифры которой он обозначал буквами латиницы.

Целые числа в позиционных системах счисления записываются в виде последовательности подряд идущих цифр: 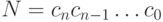$N=c_n c_{n-1}\ldots c_0$ . Эта запись стала настолько естественной, что иногда теряется ее исконный смысл: 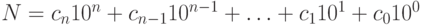$N = c_n 10^n + c_{n-1} 10^{n-1} + \ldots + c_1 10^1 + c_0 10^0$ , при котором цифры в записи числа представляют собой коэффициенты разложения числа по степеням основания, так что вклад каждой цифры в число определяется как самой цифрой, так и ее позицией и равен c_k 10^k . По причине того, что вклад каждой цифры в число зависит от ее позиции, система счисления и называется позиционной.

Запись чисел в позиционной системе легко обобщается и на числа с дробной частью: 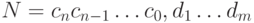$N=c_n c_{n-1}\ldots c_0,d_1\ldots d_m$ , где дробная часть отделяется от целой символом запятой или точки. И в этом случае остается справедливым разложение числа по степеням основания, в котором цифры дробной части задают коэффициенты для отрицательных степеней основания:

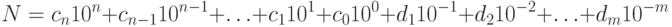$N = c_n 10^n + c_{n-1}10^{n-1} + \ldots + c_1 10^1 + c_0 10^0 + d_1 10^{-1} + d_2 10^{-2} + \ldots + d_m 10^{-m}$

( 5.1)

Понимание соотношения 5.1 достаточно для решения большинства задач, рассматриваемых в этом разделе и являющихся частными случаями следующей задачи: дано представление числа в системе с основанием , требуется найти его представление в системе с основанием . (Пример: найти запись числа $N=2BA37,5F_{(16)}$ в троичной системе счисления).

Рассмотрим возможную схему решения подобных задач. Зная основание системы счисления и цифры в записи числа в этой системе счисления, нетрудно вычислить значение числа в десятичной системе счисления. Для этого достаточно воспользоваться соотношением 5.1, в котором значения цифр и основание системы счисления задаются в десятичной системе и в ней же ведутся вычисления. Например:

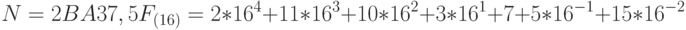
$N=2BA37,5F_{(16)} = 2*16^4 + 11*16^3 +10*16^2 + 3*16^1 +7 + 5*16^{-1} + 15*16^{-2}$

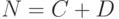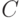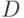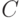Сложнее, но тоже достаточно просто решается и обратная задача. Зная значение числа в десятичной системе, нетрудно получить цифры, задающие его запись в системе с основанием . Представим число в виде суммы целой и дробной частей N=C+D . Рассмотрим схему получения цифр отдельно для целой части и дробной - . Пусть в системе с основанием число представимо в виде 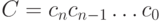$C = c_n c_{n-1}\ldots c_0$ . Тогда нетрудно получить его последнюю цифру 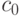c_0 и число 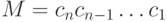$M = c_n c_{n-1}\ldots c_1$ , полученное отбрасыванием последней цифры в записи числа 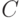. Для этого достаточно воспользоваться операциями деления нацело и получения остатка при делении нацело: $c_0 = C%p;\quad M = C/p;$

Применяя этот прием n раз, получим все цифры в записи числа 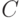. Заметьте, имеет место соотношение: 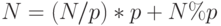$N=(N/p)*p + N \% p$ , где в соответствии с языком C# операция 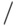означает деление нацело, а % - остаток от деления нацело. Чтобы получить все цифры и сохранить их в массиве, достаточно эту схему вставить в соответствующий цикл, что схематично можно представить следующим почти программным текстом:

M=C;  i=0;
while(M!=0)
{
  c=M%p; M=M/p; Ar[i] =c; i++;
}

Для получения цифр дробной части применяется та же схема, но с некоторой модификацией. Если цифры целой части вычисляются, начиная с последней, младшей цифры числа, то цифры дробной части вычисляются, начиная с первой цифры после запятой. Для ее получения достаточно имеющуюся дробь умножить на основание системы счисления и в полученном результате взять целую часть. Для получения последующих цифр этот процесс следует применять к числу , представляющему дробь, из которой удалена первая цифра: $d_1 =[D*p];\quad m=\{d*p\}$ . Здесь [x] и $\{x\}$ означают соответственно взятие целой и дробной части числа . Хотя напрямую этих операций нет в языке C#, но их достаточно просто выразить имеющимися средствами этого языка.

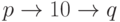Чтобы перейти от системы счисления к системе счисления , всегда ли следует использовать десятичную систему в качестве промежуточной: $p\to 10\to q$ ? Нет, не всегда. В ряде случаев удобнее использовать прием, основанный на следующем утверждении:

если основания систем счисления связаны соотношением p = q^k

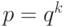, то для перехода от записи числа в системе с основанием p к записи числа в системе с основанием q достаточно каждую цифру системы p представить группой из k цифр системы q.

Для обратного перехода из q в p достаточно сгруппировать цифры системы q и каждую группу из k цифр заменить одной цифрой системы p. Доказательство этих утверждений оставляю читателю.

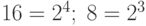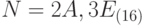Для программистов особую важность представляют три системы счисления - двоичная, восьмеричная и шестнадцатеричная, основания которых связаны упомянутым соотношением: $16 = 2^4;\; 8 = 2^3$ . Рассмотрим число , записанное в шестнадцатеричной системе $N = 2A,3E_{(16)}$ . Чтобы получить его запись в двоичной системе, каждую цифру запишем в двоичной системе, представив ее группой из четырех двоичных цифр. Нетрудно видеть, что $N = 00101010,00111110_{(2)}$ . 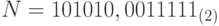Незначащие нули слева и справа могут быть отброшены, так что окончательно имеем: $N = 101010,0011111_{(2)}$ . Переведем это число в восьмеричную систему. 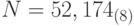Для этого достаточно провести группирование по три цифры влево и вправо от запятой соответственно для целой и дробной части, так что получим: $N = 52,174_{(8)}$ .

Римская система счисления

Еще сегодня для записи целых чисел, в особенности дат, используется римская система счисления. Эта система записи чисел не является позиционной. В ее основе лежит понятие человеческих рук с их пятью и десятью пальцами. Поэтому в этой системе есть цифры 1, 5 и 10, записываемые с помощью символов I, V, X. Помимо этого есть еще четыре цифры - 50, 100, 500, 1000, задаваемые символами L, C, D, M. В этой системе нет цифры 0, и она не является позиционной. Согласно правилам системы с помощью цифр римской системы можно записать все целые числа, не превышающие 4000. Как обычно, запись числа представляет собой последовательность подряд идущих цифр, а значением числа является сумма цифр в его записи. Например, число III означает I + I + I = 3. В записи числа старшие цифры предшествуют младшим, например, CVI = C+V+I = 100+5+1=106. Из этого правила есть одно исключение. Младшая цифра может предшествовать старшей цифре, и тогда вместо сложения применяется вычитание, например, CIX = C+X-I = 100+10-1=109.

Задачи

1. Дано целое число 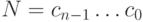$N = c_{n-1}…c_0$ , где - это цифры. Получить n - число цифр в записи числа и целочисленный массив DigitsN, такой, что .
2. Дано целое число 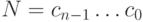$N = c_{n-1}…c_0$ , где - это цифры. Получить строку strN, задающую запись числа N. Указание: конечно, можно воспользоваться стандартным методом ToString, но в задаче требуется дать собственную реализацию этого метода.
3. Дано дробное число 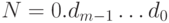$N = 0.d_{m-1}…d_0$ , где 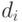- это цифры. Получить m - число цифр в записи числа и целочисленный массив FractN, такой, что .
4. Дано дробное число 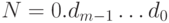$N = 0.d_{m-1}…d_0$ , где 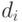- это цифры. Получить строку strN, задающую запись числа N. Указание: конечно, можно воспользоваться стандартным методом ToString, но в задаче требуется дать собственную реализацию этого метода.
5. Дано вещественное число с целой и дробной частью 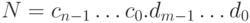$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 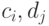- это цифры. Получить n и m - число цифр в записи целой и дробной части числа и целочисленный массив DigitsN из n+m элементов, такой, что первые его n элементов содержат цифры целой части, а последние m элементов - дробной.
6. Дано вещественное число с целой и дробной частью 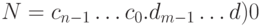$N = c_{n-1}…c_0.d_{m-1}…d)0$ , где 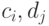- это цифры. Получить строку strN, задающую запись числа N.
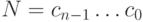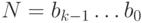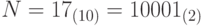
7. Дано целое число $N = c_{n-1}…c_0$ , где ci - это цифры десятичной системы счисления. Перевести число N в двоичную систему счисления $N = b_{k-1}…b_0$ , получить k - число цифр и целочисленный массив DigitsN, такой, что , где - это цифры в записи числа N в двоичной системе счисления. Пример: $N = 17_{(10)} = 10001_{(2)}$
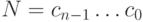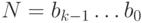8. Дано целое число $N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Перевести число N в троичную систему счисления $N = b_{k-1}…b_0$ , получить k - число цифр и целочисленный массив DigitsN, такой, что , где - это цифры в записи числа N в троичной системе счисления. Пример: $N = 17_{(10)} = 122_{(3)}$
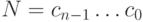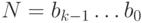9. Дано целое число $N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Перевести число N в четверичную систему счисления $N = b_{k-1}…b_0$ , получить k - число цифр и целочисленный массив DigitsN, такой, что , где - это цифры в записи числа N в четверичной системе счисления. Пример: $N = 17_{(10)} = 101_{(4)}$
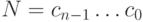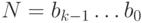10. Дано целое число $N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Перевести число N в восьмеричную систему счисления $N = b_{k-1}…b_0$ , получить k - число цифр и целочисленный массив DigitsN, такой, что , где - это цифры в записи числа N в восьмеричной системе счисления. Пример: $N = 17_{(10)} = 21_{(8)}$
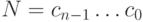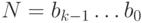11. Дано целое число $N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Перевести число N в шестнадцатеричную систему счисления $N = b_{k-1}…b_0$ , получить k - число цифр и целочисленный массив DigitsN, такой, что , где - это цифры в записи числа N в шестнадцатеричной системе счисления. Пример: $N = 17_{(10)} = 11_{(16)}$
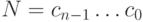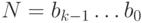12. Дано целое число $N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Перевести число N в двоичную систему счисления $N = b_{k-1}…b_0$ . Получить строку strN, задающую запись числа N. Пример: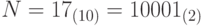 $N = 17_{(10)} = 10001_{(2)}$
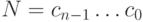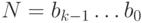13. Дано целое число $N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Перевести число N в троичную систему счисления $N = b_{k-1}…b_0$ . Получить строку strN, задающую запись числа N. Пример: $N = 17_{(10)} = 122_{(3)}$
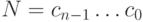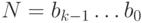14. Дано целое число $N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Перевести число N в четверичную систему счисления $N = b_{k-1}…b_0$ . Получить строку strN, задающую запись числа N. Пример: $N = 17_{(10)} = 101_{(4)}$
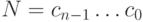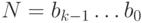15. Дано целое число $N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Перевести число N в восьмеричную систему счисления $N = b_{k-1}…b_0$ . Получить строку strN, задающую запись числа N. Пример: $N = 17_{(10)} = 21_{(8)}$
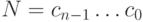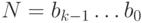16. Дано целое число $N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Перевести число N в шестнадцатеричную систему счисления $N = b_{k-1}…b_0$ . Получить строку strN, задающую запись числа N. Пример: $N = 17_{(10)} = 11_{(16)}$
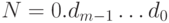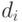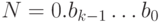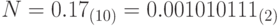17. Дано дробное число $N = 0.d_{m-1}…d_0$ , где - это цифры десятичной системы счисления. Перевести число N в двоичную систему счисления $N = 0.b_{k-1}…b_0$ , вычислив k цифр в его записи, сохраняя их в целочисленном массиве DigitsN, таком, что , где - это цифры в записи числа N в двоичной системе счисления. Пример: $N = 0.17_{(10)} = 0.001010111_{(2)}$ при k=9.
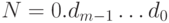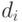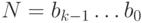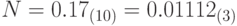18. Дано дробное число $N = 0.d_{m-1}…d_0$ , где - это цифры десятичной системы счисления. Перевести число N в троичную систему счисления $N = b_{k-1}…b_0$ , вычислив k цифр в его записи, сохраняя их в целочисленном массиве DigitsN, таком, что , где - это цифры в записи числа N в троичной системе счисления. Пример: $N = 0.17_{(10)} = 0.01112_{(3)}$ при k=5.
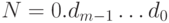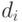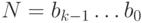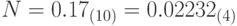19. Дано дробное число $N = 0.d_{m-1}…d_0$ , где - это цифры десятичной системы счисления. Перевести число N в четверичную систему счисления $N = b_{k-1}…b_0$ , вычислив k цифр в его записи, сохраняя их в целочисленном массиве DigitsN, таком, что , где - это цифры в записи числа N в четверичной системе счисления. Пример: $N = 0.17_{(10)} = 0.02232_{(4)}$ при k=5.
20. Дано дробное число 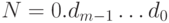$N = 0.d_{m-1}…d_0$ , где 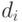- это цифры десятичной системы счисления. Перевести число N в восьмеричную систему счисления 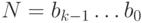$N = b_{k-1}…b_0$ , вычислив k цифр в его записи, сохраняя их в целочисленном массиве DigitsN, таком, что , где - это цифры в записи числа N в восьмеричной системе счисления. Пример: $N = 0.17_{(10)} = 0.127_{(8)}$ при k=3.
21. Дано дробное число 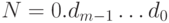$N = 0.d_{m-1}…d_0$ , где 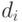- это цифры десятичной системы счисления. Перевести число N в шестнадцатеричную систему счисления 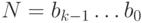$N = b_{k-1}…b_0$ , вычислив k цифр в его записи, сохраняя их в целочисленном массиве DigitsN, таком, что , где - это цифры в записи числа N в шестнадцатеричной системе счисления. Пример: $N = 0.17_{(10)} = 0.1B_{(16)}$ при k=5.
22. Дано вещественное число с целой и дробной частью 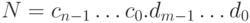$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 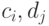- это цифры десятичной системы счисления. Перевести число N в двоичную систему счисления с заданной точностью, вычислив k цифр дробной части числа. Получить строку strN, задающую запись числа N в этой системе счисления. Пример: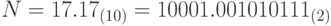 $N = 17.17_{(10)} = 10001. 001010111_{(2)}$
23. Дано вещественное число с целой и дробной частью 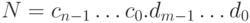$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 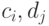- это цифры десятичной системы счисления. Перевести число N в троичную систему счисления с заданной точностью, вычислив k цифр дробной части числа. Получить строку strN, задающую запись числа N в этой системе счисления. Пример: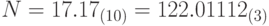 $N = 17.17_{(10)} = 122. 01112_{(3)}$
24. Дано вещественное число с целой и дробной частью 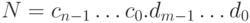$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 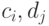- это цифры десятичной системы счисления. Перевести число N в четверичную систему счисления с заданной точностью, вычислив k цифр дробной части числа. Получить строку strN, задающую запись числа N в этой системе счисления. Пример: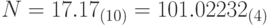 $N = 17.17_{(10)} = 101. 02232_{(4)}$
25. Дано вещественное число с целой и дробной частью 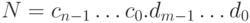$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 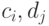- это цифры десятичной системы счисления. Перевести число N в восьмеричную систему счисления с заданной точностью, вычислив k цифр дробной части числа. Получить строку strN, задающую запись числа N в этой системе счисления. Пример: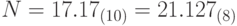 $N = 17.17_{(10)} = 21. 127_{(8)}$
26. Дано вещественное число с целой и дробной частью 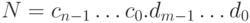$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 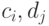- это цифры десятичной системы счисления. Перевести число N в шестнадцатеричную систему счисления с заданной точностью, вычислив k цифр дробной части числа. Получить строку strN, задающую запись числа N в этой системе счисления. Пример: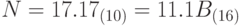 $N = 17.17_{(10)} = 11. 1B_{(16)}$
27. Дана строка, задающая представление целого числа 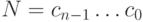$N = c_{n-1}…c_0$ , где - это цифры десятичной системы счисления. Получить число N. Эту задачу можно сформулировать и так: задайте собственную реализацию метода ToInt32 класса Convert.
28. Дана строка, задающая представление вещественного числа с целой и дробной частью: 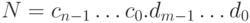$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 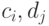- это цифры десятичной системы счисления. Получить число N. Эту задачу можно сформулировать и так: задайте собственную реализацию метода ToDouble класса Convert.
29. Дана строка, задающая в двоичной системе счисления представление целого числа 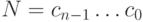$N = c_{n-1}…c_0$ , где - это цифры двоичной системы счисления. Получить число N. Эту задачу можно рассматривать, как расширение класса Convert: добавление метода FromBinaryToInt32.
30. Дана строка, задающая в двоичной системе счисления представление вещественного числа с целой и дробной частью: 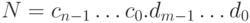$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 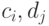- это цифры двоичной системы счисления. Получить число N. Эту задачу можно рассматривать, как расширение класса Convert: добавление метода FromBinaryToDouble.
31. Дана строка, задающая в шестнадцатеричной системе счисления представление целого числа 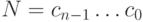$N = c_{n-1}…c_0$ , где - это цифры шестнадцатеричной системы счисления. Получить число N. Эту задачу можно рассматривать, как расширение класса Convert: добавление метода FromHexToInt32.
32. Дана строка, задающая в двоичной системе счисления представление вещественного числа с целой и дробной частью: 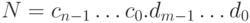$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 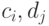- это цифры двоичной системы счисления. Получить число N. Эту задачу можно рассматривать, как расширение класса Convert: добавление метода FromHexToDouble.
33. Дана строка, задающая в двоичной системе счисления представление целого числа 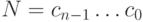$N = c_{n-1}…c_0$ , где - это цифры двоичной системы счисления. Получить строки str4N, str8N, str16N, задающие представление числа N в системах счисления: четверичной, восьмеричной, шестнадцатеричной. Указание. Используйте группирование цифр при переводе из одной системы счисления в другую.
34. Дана строка, задающая в двоичной системе счисления представление вещественного числа с целой и дробной частью: 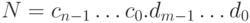$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 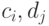- это цифры двоичной системы счисления. Получить строки str4N, str8N, str16N, задающие представление числа N в системах счисления: четверичной, восьмеричной, шестнадцатеричной. Указание. Используйте группирование цифр при переводе из одной системы счисления в другую.
35. Дана строка, задающая в восьмеричной системе счисления представление целого числа 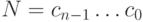$N = c_{n-1}…c_0$ , где - это цифры восьмеричной системы счисления. Получить строки str4N, str2N, str16N, задающие представление числа N в системах счисления: четверичной, двоичной, шестнадцатеричной. Указание. Используйте группирование цифр при переводе из одной системы счисления в другую.
36. Дана строка, задающая в восьмеричной системе счисления представление вещественного числа с целой и дробной частью: 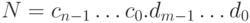$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 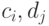- это цифры восьмеричной системы счисления. Получить строки str4N, str2N, str16N, задающие представление числа N в системах счисления: четверичной, двоичной, шестнадцатеричной. Указание. Используйте группирование цифр при переводе из одной системы счисления в другую.
37. Дана строка, задающая в шестнадцатеричной системе счисления представление целого числа 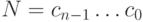$N = c_{n-1}…c_0$ , где - это цифры шестнадцатеричной системы счисления. Получить строки str4N, str8N, str2N, задающие представление числа N в системах счисления: четверичной, восьмеричной, двоичной. Указание. Используйте группирование цифр при переводе из одной системы счисления в другую.
38. Дана строка, задающая в шестнадцатеричной системе счисления представление вещественного числа с целой и дробной частью: 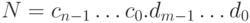$N = c_{n-1}…c_0.d_{m-1}…d_0$ , где 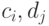- это цифры шестнадцатеричной системы счисления. Получить строки str4N, str8N, str2N, задающие представление числа N в системах счисления: четверичной, восьмеричной, двоичной. Указание. Используйте группирование цифр при переводе из одной системы счисления в другую.
39. (*) Заданы p и q - основания двух систем счисления, strN - строка, задающая представление вещественного числа N в системе с основанием p. Получить строку, задающую представление числа N в системе с основанием q, возможно, с некоторой точностью, заданной параметром k - числом цифр дробной части числа N при его записи в системе с основанием q.
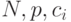40. (*) Дано число N и основание системы счисления p. Получить - коэффициенты разложения числа N по степеням основания с заданной точностью Eps. Указание. В данной задаче предполагается, что являются вещественными числами и для выполняется условие ( 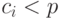). Пример: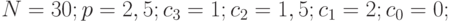
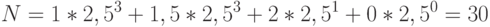
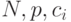41. Дано основание системы счисления p и - коэффициенты разложения числа N по степеням основания. Получить число N. Указание. В данной задаче предполагается, что являются вещественными числами и для выполняется условие ( 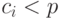). Пример:
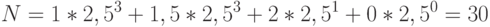
42. (*) Дана строка strRome, задающая представление целого числа N, меньшего 4000, в непозиционной римской системе счисления. Получить число N. Пример: N= MMIV = 2004
43. (*) Дано целое число N, меньшее 4000. Получить строку strRome, задающую представление числа в непозиционной римской системе счисления. Пример: N=2005 =MMV

Именованные числа

С давних пор числа применяются для измерения физических величин - длин, площадей, объемов. Как правило, при этом использовалась системы, вовсе не основанные на десятичной системе, а связанные с реально применяемыми мерами - бочонками, мешками и прочей применяемой тарой. Метрическая система мер, основанная на десятичной системе счисления, завоевала свои позиции лишь в последние два столетия, и мы стали применять километры и килограммы, килоджоули и килогерцы. Но рецидивы все еще дают себя знать, и примером тому является программисты, которые сравнительно недавно ввели систему мер для измерения объема информации. У нас байт равен 8 битам, а килобайт равен не 1000 байтов, как мог бы ожидать человек, далекий от программирования, а 1024 байта. И связано это с любовью компьютеров к двоичной системе счисления, в которой 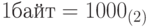$1 байт = 1000_{(2)}$ битов, а $1 Кб = 10000000000_{(2)}$ байтов.

Задачи

44. Задано число T (температура) и единица измерения (C - градусы по Цельсию, F - по Фаренгейту, R - по Реомюру, K - по Кельвину). Определить значения температуры в других шкалах, используя следующие соотношения:
$T_F=1,8T_C+32;\quad T_R=0,8T_C;\quad T_K=T_C+273,2;$
Пример:
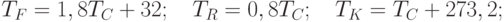
45. Дано число N, задающее расстояние, измеренное с точностью до долей миллиметра. Получите строку, задающую расстояние с использованием старинной китайской системы, в которой справедливы следующие соотношения:
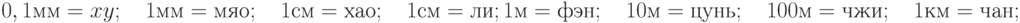
$0,1мм=xy;\quad 1мм=мяо;\quad 1см=хао;\quad 1см=ли;\\ 1м=фэн;\quad 10м=цунь;\quad 100м=чжи;\quad 1км=чан;$
46. Дано число N, задающее расстояние, измеренное с точностью до долей миллиметра. Получите строку, задающую расстояние с использованием старинной древнерусской системы, в которой справедливы следующие соотношения:
$1вершок=44,45мм;\quad 1четверть=4вершка;\quad 1аршин=4четверти;\\ 1сажень=3аршина;\quad 1верста=500саженей;\quad 1миля=7верст.$
47. Дано число N, задающее расстояние, измеренное с точностью до долей миллиметра. Получите строку, задающую расстояние с использованием английской системы мер длины, в которой справедливы следующие соотношения:
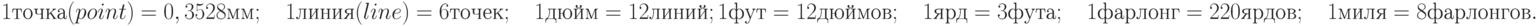
$1точка(point)=0,3528мм;\quad 1линия(line)=6точек;\quad 1дюйм=12линий;\\ 1фут=12дюймов;\quad 1ярд=3фута;\quad 1фарлонг=220ярдов;\quad 1миля=8фарлонгов.$
48. Дано вещественное число N, задающее объем хранимых данных в терабайтах. Выразите значение N в гигабайтах, мегабайтах, килобайтах, байтах, битах.