От встроенных систем к системам интеллектуальным
Соединение процессов обработки данных и управления в интеллектуальных встроенных устройствах
Сложившаяся к настоящему времени парадигма использования вычислительных устройств базируется на исторически сложившемся разделении процессов обработки данных и принятия управленческих решений (после обработки). Основания этого разделения прослеживаются в истории развития средств вычислительной техники. Первоначально компьютеров было мало и они, занимая огромные пространства, требовали специальных условий для эксплуатации. Формировались особые вычислительные центры для объединенного решения в одном месте множества разных задач, причем до сих пор актуальным остается одно из приоритетных направлений развития – создание суперкомпьютеров. Встроенным устройствам традиционно отводилась роль или устройств для сбора данных, или устройств для реализации определенных управляющих воздействий. В некоторых случаях они использовались как регуляторы в простых контурах обратной связи. Суперкомпьютеры брали на себя выполнение задач Data Mining.
Но надо четко отдавать себе отчет в применимости этой традиционной парадигмы. В природе и обществе все-таки информационно-управленческие связи являются основой всех явлений и процессов. Искусственно разделяя процессы обработки данных и управления, мы существенно снижаем наши потенциальные возможности использования информационно-коммуникационных технологий.
Надо ли разделять процессы обработки данных и управления? С начала XXI века в теории управления заметен всплеск интереса к тематике управления в сетях, коллективному взаимодействию, мультиагентным технологиям и т.п. Это во многом связано с технологическим прогрессом. Сейчас миниатюризация и быстродействие средств вычислительной техники достигли такого уровня, что стало возможным в миниатюрных встроенных системах реального времени использовать вычислительные блоки, соизмеримые по производительности с мощными компьютерами XX в. Все чаще "простые" встроенные устройства заменяются на "интеллектуальные встроенные системы".
Новые альтернативы позволяют по-новому взглянуть на ставшую уже традиционной область Data Mining.
В литературе все чаще появляются мысли о возрождении науки "Кибернетика" с большой буквы, о появлении "неокибернетики" (Б.В. Соколов, Р.М. Юсупов). Теория управления, начавшись с регуляторов механических систем в ХIХ в., пройдя к концу ХХ в. этап глубокой интеграции с цифровыми технологиями обработки данных и принятия решений, фокусируясь в ХХI в. на сетях объектов, выступает "собирателем" трех основных компонент прогресса второй половины ХХ века:
- теории управления (Control Theory),
- теории коммуникаций (Communication Theory)
- информатики (Computer Science) (Б.Р. Андриевский, А.С. Матвеев, А.Л. Фрадков).
Может ли дать какое-то новое качество в обработке данных и извлечении знаний применение кибернетической парадигмы, при которой процессы "добычи знаний" и получения информации будут учитывать неразрывную связь информации и управления (и опираться на нее)?
Да, может!!!
Для иллюстрации положительного ответа в статье О.Н. Граничина (2012) рассмотрены несколько примеров повышения эффективности процессов обработки данных и управления при изменении парадигмы, основанных на рандомизации управляющих воздействий и использовании замкнутых стратегий управления в условиях неопределенностей. Остановимся на одном из них.
Эффективность замкнутых стратегий в условиях неопределенностей.Рассмотрим объект управления (ОУ) с входами 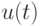 и выходами
и выходами 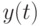 , и предположим, что задано начальное состояние
, и предположим, что задано начальное состояние  , и динамика объекта при
, и динамика объекта при 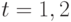 описывается уравнением
описывается уравнением
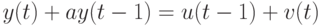
с неопределенностями 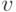 и
и  типов:
типов:
- динамические возмущения
 неизвестны и ограничены для всех
неизвестны и ограничены для всех 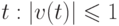 , но могут меняться со временем;
, но могут меняться со временем; - коэффициент модели
 также неизвестен и ограничен:
также неизвестен и ограничен: ![a \in \left[ 1;5 \right]](/sites/default/files/tex_cache/876c6924cb6dde13a530bed0f94a831e.png) ,но он не может изменяться со временем.
,но он не может изменяться со временем.
Мы можем выбирать входы  и
и 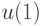 . Пусть наша цель – минимизировать
. Пусть наша цель – минимизировать  . Рассмотрим минимаксный функционал качества:
. Рассмотрим минимаксный функционал качества:
![J=sup_{a \in \left[ 1;5 \right]}sup_{\left | v(1)\right |\leqslant 1,\left | v(2)\right |\leqslant 1}\left | y(2)\right | \rightarrow min_{u(0)\mu(1)}](/sites/default/files/tex_cache/da6d4ce8c20372a84040a01aac31ecb5.png)
Конечно, это пример не для супервычислений. Мы специально выбрали достаточно простую модель и рассматриваем всего два шага по времени t = 1,2, с тем чтобы решить задачу почти устно. Но если рассмотреть t = 1,2,3, то сложность серьезно возрастает, а при больших t несколько лет тому назад одному из моих дипломников не хватило времени для решения задачи не только на персональном компьютере, но и с привлечением дополнительных вычислительных ресурсов нашего университета.
Мы сравним качество минимаксной оптимизации для двух классов допустимых стратегий управления
- программное управление,
- замкнутое управление.
Программное управление. Этот класс состоит из всевозможных пар 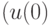 ,
, 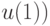 . Для того чтобы выбрать
. Для того чтобы выбрать 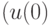 и
и 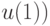 , перепишем функционал качества в соответствии с уравнением ОУ как функцию от
, перепишем функционал качества в соответствии с уравнением ОУ как функцию от 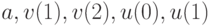 :
:
![J=sup_{a \in \left[ 1;5 \right]}sup_{\left | v(1)\right |\leqslant 1,\left | v(2)\right |\leqslant 1}\left | a^2-au(0)+av(1)+u(1)+v(2)\right |](/sites/default/files/tex_cache/f5c996c5ac9a3562e33e986b41426896.png)
Произведя максимизацию по отношению к  ,
, 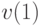 и
и 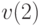 , получаем функцию от переменных
, получаем функцию от переменных  и
и 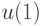 . Минимизация этой функции по
. Минимизация этой функции по  и
и 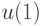 дает значения
дает значения 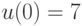 ,
, 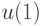 = 12,25 и
= 12,25 и
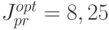
Замкнутое управление. В момент времени t = 1 мы получаем выход 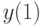 и знаем предыдущее управление
и знаем предыдущее управление  . Замкнутые стратегии управления определяются парой
. Замкнутые стратегии управления определяются парой  и функцией обратной связи
и функцией обратной связи 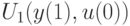 . При фиксированных входе
. При фиксированных входе 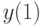 и управлении
и управлении  с силу уравнения ОУ и условия
с силу уравнения ОУ и условия 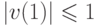 выполняется следующее неравенство:
выполняется следующее неравенство:
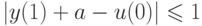
Следовательно, можно определить интервал
![\left [ a^-;a^+ \right ]=\left [1;5 \right ] \bigcap \left [ -1+u(0)-y(1);1+u(0)-y(1)\right ]](/sites/default/files/tex_cache/db61b82afe23971d1ad4829755e34f16.png)
который гарантированно содержит параметр a, и его границы вычисляются по формулам:
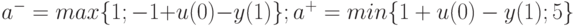
Для оптимального выбора 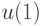 функционал качества можно переписать как функцию от
функционал качества можно переписать как функцию от 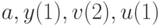 :
:
![J=sup_{a \in \left[ 1;5 \right]}sup_{\left | v(1)\right |\leqslant 1}( sup_{a \in [a^-;a^+]} sup_{\left | v(2)\right |\leqslant 1}\lvert - ay(1)+u(1)+v(2)\rvert)](/sites/default/files/tex_cache/45856589598485bc2edff698abac3841.png)
Минимизация по 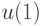 приводит к формуле
приводит к формуле
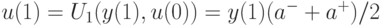
учитывая которую, получаем
![J=sup_{a \in \left[ 1;5 \right]}sup_{\left | v(1)\right |\leqslant 1}\lvert y(1)(a^-+a^+)/2+1\rvert](/sites/default/files/tex_cache/606f3bc187d355947cb2409428f72a5a.png) После исключения
После исключения 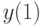 в силу уравнения ОУ, произведя операции максимизации, мы можем переписать
в силу уравнения ОУ, произведя операции максимизации, мы можем переписать 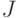 как функцию от
как функцию от  .
.
Минимизация по  дает значение
дает значение 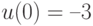 и
и 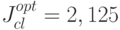 .В итоге имеем
.В итоге имеем
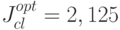 <<
<<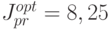
Зависимость качества управления от задания класса неупреждающих стратегий адекватно понимается далеко не всех публикациях. Если все параметры объекта управления известны и помехи отсутствуют, то множества программных и замкнутых стратегий управления оказываются совпадающими.
Основатель кафедры теоретический кибернетики СПбГУ В.А. Якубович любил приводить еще и такую шутку о связи процессов обработки данных и управлений: как-то раз две мышки на молочной ферме одновременно упали с полки с сырами и угодили в неполные бидоны с молоком (в два разных). Задача у них – выжить. Время сильно ограничено, под поверхностью дышать они не могут, а сил "барахтаться" на много не хватит. Возможны две стратегии:
- анализировать ситуацию, смотреть на уходящую вверх ровную стенку бидона и пытаться придумать способ как выжить;
- начать активно "барахтаться", пытаться что-то предпринимать, физически бороться за жизнь.
Первая мышка утонула, так и не придумав способ как выжить. У второй молоко в бидоне "взбилось" и превратилось в густую сметану, на поверхности которой мышка прожила пару дней и в конце концов нашла способ выбраться из бидона.
