Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3978 / 1247 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Специальности: Программист, Математик
Теги:
Лекция 2:
Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования
1.1. Обусловленность задачи
Пример 1.1. Вычислить все корни уравнения
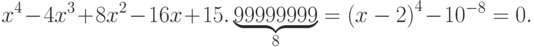
Точное решение задачи легко найти:
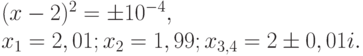
Если компьютер работает при 
, то свободный член в исходном уравнении будет округлен до 16,0 и, с точки зрения представления чисел с плавающей точкой, будет решаться уравнение (x-2)4= 0, т.е. x1,2,3,4 = 2, что, очевидно, неверно. В данном случае малые погрешности в задании свободного члена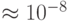 
привели, независимо от метода решения, к погрешности в решении 
Пример 1.2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:
u''(t) = u(t), u(0) = 1, u'(0) = - 1.
Общее решение имеет вид
u(t) = 0,5[u(0) + u'(0)]et + 0,5[u(0) - u'(0)]e- t.
При заданных начальных данных точное решение задачи: u(x) =
e-t, однако малая погрешность 
в их задании приведет к появлению члена 
, который при больших значениях аргумента может существенно исказить решение.
Пример 1.3. Пусть необходимо найти решение обыкновенного дифференциального уравнения
![u^{\prime} = 10u,\quad u = u(t),\\
u(t_0) = u_0,\quad t \in [0,1].](/sites/default/files/tex_cache/b49a6989048f6e216be9eef7e6de646e.png)
Его решение: 
, однако значение u(t0) известно лишь приближенно: 
, и на самом деле 
Соответственно, разность u* - u будет
Предположим, что необходимо гарантировать некоторую заданную точность
вычислений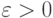 
всюду на отрезке ![t \in [0,1].](/sites/default/files/tex_cache/f7e36b3d9282ae855a03f40641a086cc.png)
Тогда должно выполняться условие
Очевидно, что
![\max\limits_{t \in [0,1]} |{u^*(t) - u(t)}| = |{u*(1) - u(1)}| =
|{u_0^* - u_0}|e^{10(1 - t_0)}.](/sites/default/files/tex_cache/4e40d8aa3cb5c5b4619e211d1ae708cb.png)
Отсюда можно получить требования к точности задания начальных данных 
при t0= 0.
Таким образом, требование к заданию точности начальных данных оказываются в e10 раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.
Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.
Пример 1.4. Решением системы линейных алгебраических уравнений (СЛАУ)
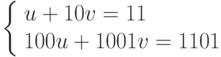
является пара чисел {1, 1}.
Изменив правую часть системы на 0,01, получим возмущенную систему
с решением {11.01; 0.00}, сильно отличающимся от решения невозмущенной системы. Эта система также плохо обусловлена.
Пример 1.5. Рассмотрим полином
(x - 1)(x - 2)...(x - 20)=x20 - 210x19 + ...,
корни которого x1 = 1, x2 = 2, …, x20 = 20.
Положим, что коэффициент (-210) при x19
увеличен на 
В результате вычислений с 11-ю значащими цифрами получим совершенно иные корни: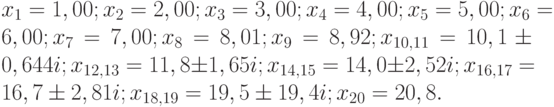 
Причина значительного расхождения также заключается в плохой обусловленности задачи вычисления корней рассматриваемого выражения.
