Системы линейных уравнений
Приведение системы линейных уравнений с помощью элементарных преобразований к ступенчатому виду
Определение 3.5.1 (определение ступенчатой матрицы (системы)). Под ступенчатой системой линейных уравнений понимается система линейных уравнений со ступенчатой матрицей коэффициентов, т. е.:
- все нулевые строки находятся в матрице ниже ненулевых строк;
- если (0,...,0,aik,...,ain),
 - первый ненулевой элемент в i -й строке (называемый лидером i -й строки), то ars=0 для всех
- первый ненулевой элемент в i -й строке (называемый лидером i -й строки), то ars=0 для всех 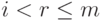 ,
, 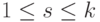 (элементы ars=0 для всех мест (r,s), расположенных в строчках, ниже i -й, и в столбцах s=1,2,...,k ). Другими словами, лидер строки с большим номером стоит строго правее.
(элементы ars=0 для всех мест (r,s), расположенных в строчках, ниже i -й, и в столбцах s=1,2,...,k ). Другими словами, лидер строки с большим номером стоит строго правее.
Определение 3.5.2. Ненулевая матрица 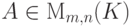 имеет главный ступенчатый вид, если матрица A имеет ступенчатый вид, все лидеры ненулевых строк
имеет главный ступенчатый вид, если матрица A имеет ступенчатый вид, все лидеры ненулевых строк 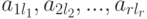 (
( 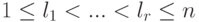 ) равны 1 и для каждого j,
) равны 1 и для каждого j, 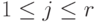 , в lj -м столбце матрицы A единственный ненулевой элемент - это
, в lj -м столбце матрицы A единственный ненулевой элемент - это 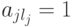 .
.
Примеры 3.5.3. Матрица
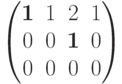
Матрица
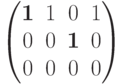
Нулевая матрица имеет ступенчатый вид.
Матрица

Матрицы
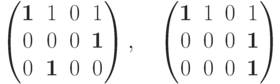
Замечание 3.5.4. Свойство быть ступенчатой матрицей алгоритмически (с помощью компьютера) распознаваемо.
Лемма 3.5.5. Пусть 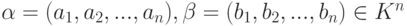 , ak - лидер строки
, ak - лидер строки  , bl - лидер строки
, bl - лидер строки  ,
,  , cm - лидер строки
, cm - лидер строки 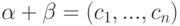 , ci=ai+bi,
, ci=ai+bi, 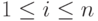 . Тогда:
. Тогда:
-
 ;
; - если k<m, то k=l.
Доказательство.
- Так как
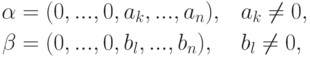
 ,
тои поэтому
,
тои поэтому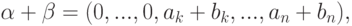
 (если bk=-ak, то ak+bk=0, и тогда k<m ).
(если bk=-ak, то ak+bk=0, и тогда k<m ). - Пусть k<m. Если k<l, то bk=0,и поэтому k = m, что противоречит k<m.
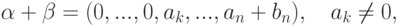
Итак, k=l.
Следствие 3.5.6. Пусть 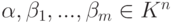 ,
, 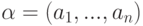 ,
, 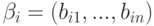 ,
,  ,
, 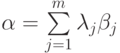 ,
,  ,
,  - лидер строки
- лидер строки  ,
, 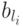 - лидер строки
- лидер строки 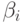 . Тогда
. Тогда  .
.
Теорема 3.5.7 (алгоритм Гаусса). Всякую систему линейных уравнений конечным числом элементарных преобразований 1-го и 2-го типов можно привести к ступенчатому виду (т. е. к системе линейных уравнений, матрица коэффициентов которой является ступенчатой матрицей).
Доказательство. Можно считать, что не все коэффициенты aij равны нулю и, более того, что при x_1 (т. е. в первом столбце матрицы коэффициентов) есть ненулевой элемент 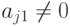 (в противном случае можно перейти к системе от переменных x2,...,xn ). Если a11=0, то, переставляя 1 -е и j -е уравнения (строки расширенной матрицы) (т. е. совершая преобразование 2-го типа), приходим к случаю, когда
(в противном случае можно перейти к системе от переменных x2,...,xn ). Если a11=0, то, переставляя 1 -е и j -е уравнения (строки расширенной матрицы) (т. е. совершая преобразование 2-го типа), приходим к случаю, когда 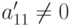 .
.
Для i=2,3,...,m последовательно проведем преобразования 1-го типа

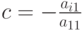 ). Тогда
). Тогда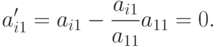
 уравнения, если среди коэффициентов есть ненулевые (пусть k - первый столбец с ненулевым элементом alk' среди a2k',...,amk' ), повторим нашу процедуру: переставим второе уравнение (строку) с l -м уравнением (строкой) и обеспечим нули ниже коэффициента a2k'.
уравнения, если среди коэффициентов есть ненулевые (пусть k - первый столбец с ненулевым элементом alk' среди a2k',...,amk' ), повторим нашу процедуру: переставим второе уравнение (строку) с l -м уравнением (строкой) и обеспечим нули ниже коэффициента a2k'.Этот процесс остановится в том случае, когда все коэффициенты при переменных в оставшихся уравнениях равны нулю.
Итак, окончательная получившаяся система линейных уравнений будет иметь ступенчатый вид (т. е. матрица коэффициентов при переменных x1,x2,...,xn будет иметь ступенчатый вид).
![\begin{equation}\label{ep15}
\left\{
\begin{array}{@{}l@{{}+...+{}}l@{{}+{}}l@{{}+{}}l@{{}+...+{}}l@{{}={}}l@{}}
\boldsymbol{\bar{a}_{11}x_1} & ... & ... & ... &
\bar{a}_{1n}x_n & \bar{b}_1,\\
0x_1 & \boldsymbol{\bar{a}_{2k}x_k} & ... & ... &
\bar{a}_{2n}x_n & \bar{b}_2,\\
\multicolumn{6}{c}{\dotfill}\\
0x_1 & ... & \boldsymbol{\bar{a}_{sl}x_l} & ... &
\bar{a}_{sn}x_n & \bar{b}_s,\\
\multicolumn{6}{c}{\dotfill}\\
0x_1 & ... & ... & \boldsymbol{\bar{a}_{rt}x_t} &
\bar{a}_{rn}x_n & \bar{b}_r,\\[2mm]
\hline
\rule{0pt}{6mm}0x_1 & ... & ... & ... & 0x_n &
\bar{b}_{r+1},\\
\multicolumn{6}{c}{\dotfill}\\
0x_1 & ... & ... & ... & 0x_n & \bar{b}_m.
\end{array}
\right.\vspace{-3mm}
\end{equation}](/sites/default/files/tex_cache/eb4b58bca390dd5312866cdb97ecf1d9.png) |
( 3.2) |
Замечания 3.5.8.
- Важный инвариант - число r уравнений в ступенчатом виде с ненулевыми коэффициентами при переменных, т. е. число "ступенек",
 . Возможен случай r=m (т. е. блок уравнений с нулевыми коэффициентами при x1,...,xn отсутствует). Независимость числа r от способа приведения к ступенчатому виду будет установлена позже (это - ранг матрицы коэффициентов).
. Возможен случай r=m (т. е. блок уравнений с нулевыми коэффициентами при x1,...,xn отсутствует). Независимость числа r от способа приведения к ступенчатому виду будет установлена позже (это - ранг матрицы коэффициентов). - Можно было бы продолжить процесс приведения к ступенчатому виду для расширенной матрицы системы линейных уравнений.
Следствие 3.5.9. Всякая система линейных уравнений эквивалентна некоторой ступенчатой системе линейных уравнений.
Следствие 3.5.10. Каждую матрицу элементарными преобразованиями строк 1-го и 2-го типа можно привести к ступенчатому виду.
